Binary Indexed Trees (also known as Fenwick Trees) are useful for finding sum ranges between two elements in a set of numbers, particularly when we need to update the numbers often. If we have a static set of values then we can just pre-compute cumulative sums and then to get a range between i and j we would do sums[j]-sums[i-1]. However, if one of the numbers changes then we have to update O(n) values in the sums array. The Binary Indexed Tree (BIT) is useful as we can quickly update values in O(log n) time and quickly query sum ranges in O(log n) time. It is quite compact as it just uses an array with an element for each number in our input set. The logic for updating and reading is also concise with just a few lines for each.
I have created a slideshow with the steps to create a BIT and the steps to query the BIT to calculate sum ranges. Click through to see the actual slideshow:
https://adamk.org/BinaryIndexedTreeAnimation/BinaryIndexedTree.html
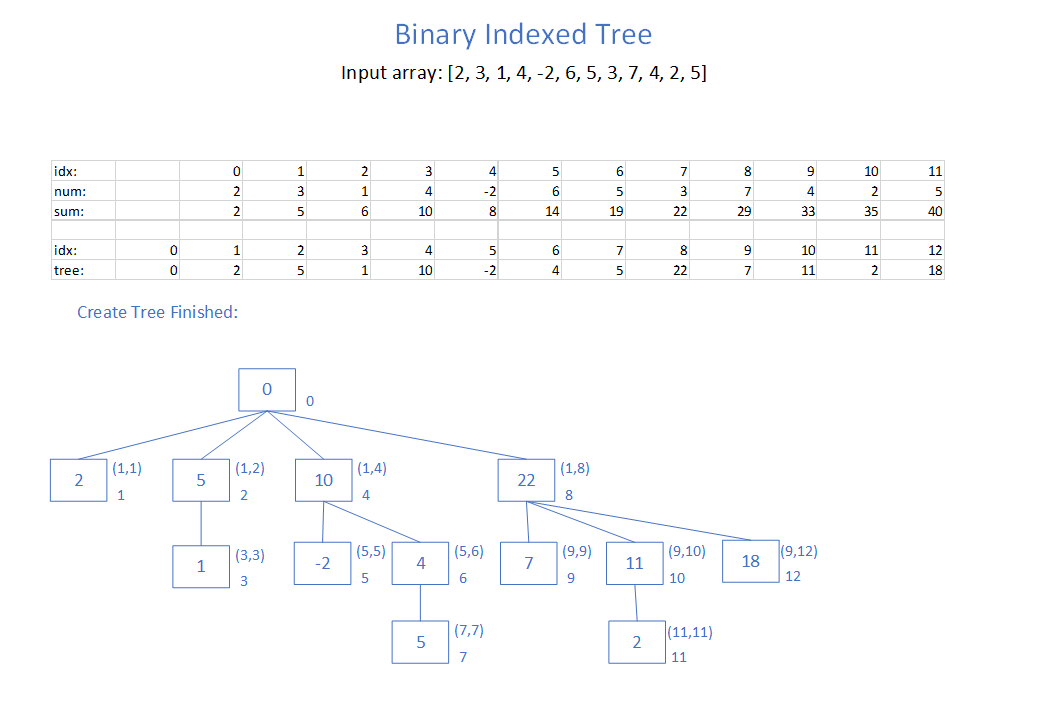
Additional BIT information:
https://www.topcoder.com/community/competitive-programming/tutorials/binary-indexed-trees/
https://www.youtube.com/watch?v=CWDQJGaN1gY (Tushar Roy)