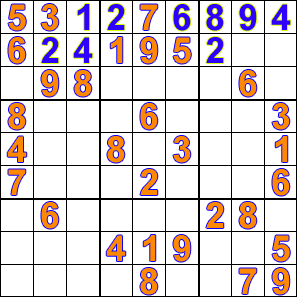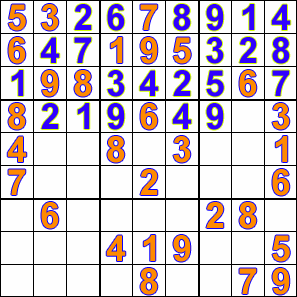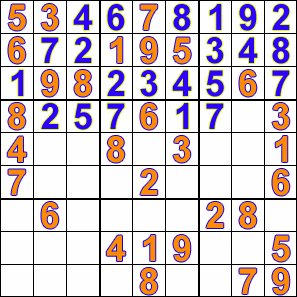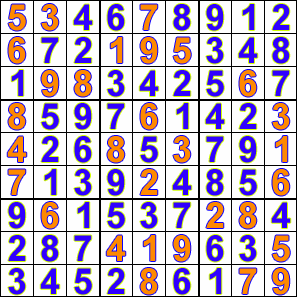
This was an interesting problem that highlights that sometimes it is better to write an algorithm for a computer to execute in a different way to how we would solve the problem with a human mind. So I first attempted to code this in a way in which I would manually solve a sudoku puzzle by walking through each number and analysing the impact of rows and columns on boxes. This resulted in complicated code and did not work on hard sudoku puzzles.
My second attempt at a solution used backtracking. The result was simpler code and the ability to solve the hardest sudoku puzzles. The algorithm stops at every space sequentially and tries every number until it finds a number that results in a valid board. If it gets to a square where no number will work then it backtracks to the previous square and continues its search through the numbers. Here is a nice visualisation of backtracking from wikipedia:
Here is my c++ source code for the solution:
We can optimise lookups when we are checking when a cell is valid. So instead of iterating through 9 values in the 3 different dimensions, we can store the presence of those 9 values in 3 vector of bools. We test the presence by looking in index of value-1. This does complicate the code somewhat as we now have a separate set of data to maintain.