Time complexity: O(nlogn)
The most common way to implement Merge Sort is with recursion:
https://gist.github.com/adamkorg/99cae1fa4da0bc8431d040c1e8f516fd
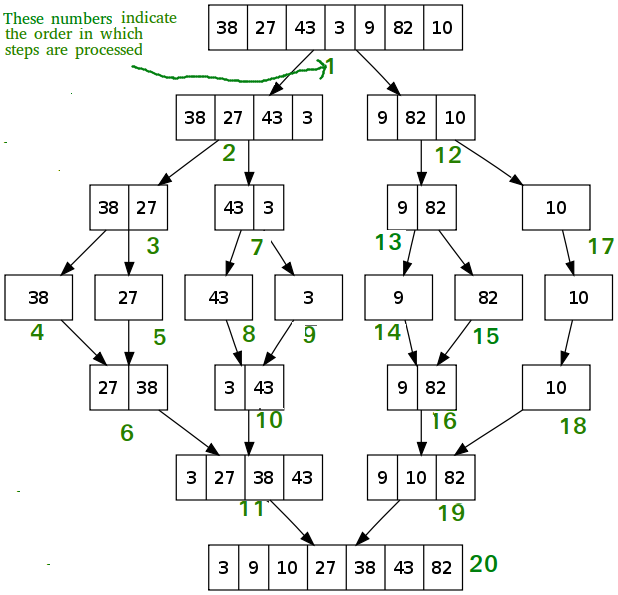
This uses divide and conquer. Divide in half repeatedly until we have list of single elements. Then we start comparing those elements to build up a set of pairs. Then we compare pairs to have sets of 4 elements. Repeat comparing/combining lists until we have a single sorted list.
In my code example I have used a mid point m as being the first element of the right hand partition. Most implementations use a mid point m as being the last element of the left hand partition but it doesn’t make a huge difference.
See the following for the sequence of recursive executions:
An alternative is to use an iterative algorithm. It uses similar merging logic but has a different way of arriving at which two subsets to use. The iterative solution starts comparing individual elements, which I call chunk size 1. Then it doubles the chunk size with each merge pass. Something to note is that the remainder needs to be adjusted if it is less than chunk size. Here’s my version:
https://gist.github.com/adamkorg/5a18047fb9ac6e0ddd16c8776e43a195
