It’s easy to implement a 2^n recursive solution and also easy to implement an iterative O(n) solution but implementing an O(log n) solution is trickier. The following has a nice summary of various solutions:
https://www.geeksforgeeks.org/program-for-nth-fibonacci-number/
I just wanted to add some commentary to matrix solution is Method 4 and 5 above. Here are my whiteboard notes/calculations:

So the key thing is to realise that raising the base matrix below to the power of n will give a value for the nth fibonacci number:
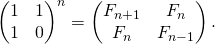
One part of the implementation challenge is dealing with matrices and doing multiplication on them. The other part of the challenge is raising the matrices to a power efficiently. A naive power function will result in O(n) but we can optimise that function to O(log n). This is normally done recursively but can be simulated iteratively using binary operators – see section 4 of the following for an implementation:
https://www.techiedelight.com/power-function-implementation-recursive-iterative/
