I have always intuitively shied away from using recursion in my code wherever possible. The few times I have had to implement it were mainly in some form of tree traversal logic. I am a little uncomfortable in relying on intuition, so in this post I’m going to flesh out my thoughts on recursion.
In certain scenarios a recursive implementation is very concise. Let’s take a look at a recursive Merge Sort:
This is very concise but the recursive logic calls are difficult to follow. The best representation of this I’ve found is this from geeksforgeeks.com:
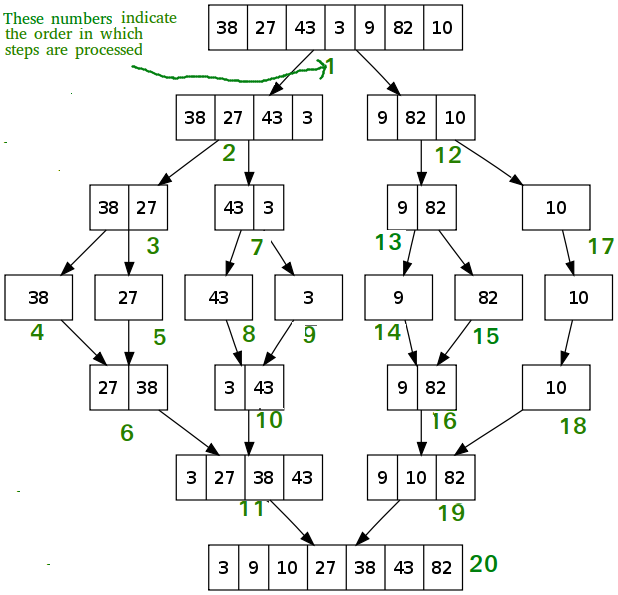
From: https://www.geeksforgeeks.org/merge-sort/
This is quite elegant how the numbers get split up through the recursive calls and then get merged as the recursive calls unwind. It is however not intuitive by looking at the source code and requires some thought, thinking through the recursive call tree. The other disadvantage is the inherent limitations of recursive calls, i.e. the overhead of the recursive calls and stack size limit which limits the scalability for large data sets.
Lets compare this to an iterative implementation:
I’ve used more descriptive variable names and comments here, so the comparison is not completely fair. Both the recursive and iterative solutions rely on a merge function not shown, but these would have similar logic. The key difference is that, once you get past the extra code, the iterative implementation is intuitively easier to understand as you don’t have to think through the recursive call tree.
It is interesting that most descriptions of merge sort default to a recursive implementation. I would argue that the iterative solution is easier to understand and implement. The recursive solution is an interesting learning exercise in the way the recursive call tree unravels.
In some cases implementing an iterative alternative to a recursive algorithm requires using a stack data structure. An example is an iterative version of a quick sort, which repeatedly pushes the two partition dimensions to a stack and then repeatedly pops elements off the stack and does a partition again:
I should note that there are some rare cases where a recursive algorithm doesn’t have an iterative alternative, e.g. the Ackermann function. I believe the correct terminology is that the Ackermann function is a total computable function (which means it is recursive) but is not primitive recursive (which means it has no iterative alternative).
https://en.wikipedia.org/wiki/Ackermann_function
So to summarise I would say recursive implementations, compared to iterative alternatives, tend to be:
– less intuitive
– less efficient
– less scalable
